Making a perfect minesweeper solver
A small project that somewhat efficiently (<1s even for large boards) can solve any Minesweeper board that can be solved deterministically, with scope to add probability-based checking.
Today, I made a perfect Minesweeper solver, with an algorithm that is fairly well optimised (sub 1s solves).
This algorithm can also be modified to find probabilities of a cell containing a mine or not.
What is Minesweeper?

Some ideas for solving minesweeper
Minesweeper has some obvious tactics.
For example, if a square has \(n\) mines around it, and \(n\) squares are covered around the square, we can deduce that they all have mines.
Similarly, if we know the positions of \(n\) mines around a square with \(n\) on it, we know that the rest of the squares must not contain mines, and so we can uncover it.
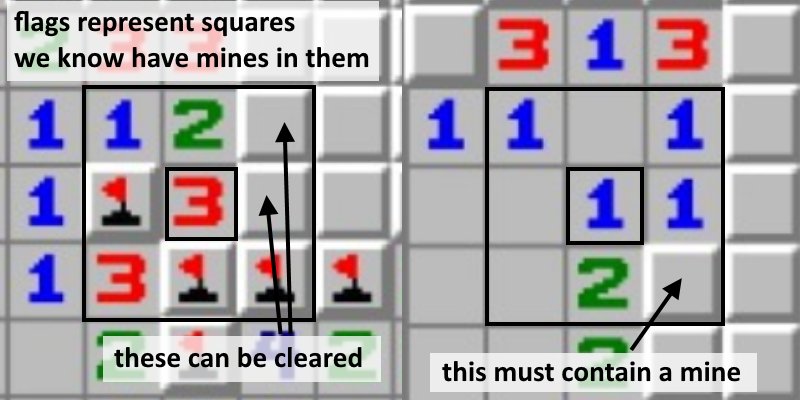
However, this basic solving can only get you so far. Here is an example of a deduction that can be made, but cannot be made with the basic ideas.

This above scenario actually does have a deduction to be made.
Let \(a\) be 1 if it has a mine under it, and 0 otherwise. Define \(b\) and \(c\) similarly.
Now the orange 1 allows us to form the equation \(a + b = 1\), and the purple 2 allows us to form the equation \(a + b + c = 2\).
Subtracting these equations from each other gives \(c = 1\), allowing us to deduce that square c has a mine under it.
This obviously pushes us to try and form a system of simultaneous equations, and then try to find solutions to these. However, I struggled with implementing this, and eventually decided against this, opting instead for a more simple “try all combinations” approach. This approach also gives a simple method to calculate probabilities of a cell having a mine or not.
Details of the combinatorial approach
Obviously, if we can uncover/flag any cells directly from the simple approach, we should do that to try to get more information. However, we will otherwise have to fall back to a trying all options approach.
Note that the only uncovered cells that we have information on are ones that are adjacent to a square with a number in it. All other cells have no information on them (apart from the total mine count, but we’ll get to that later).
This means that every step, my algorithm only needs to check covered cells adjacent to (including diagonally adjacent to) uncovered cells.

The most naive approach would be to try all \(2^n\) (where \(n\) is the number of red squares) options. However, this has some obvious inefficiencies.
For example, in the board above, half of all \(2^n\) possibilities will fail to put a mine in the isolated red square. Many of the possibilities are invalid, so this could obviously use some pruning.
To do this, we will use recursion. This algorithm will walk through all valid possibilities of mine assignments to the red squares. We will store in our recursion what is our current assignment of mines to red squares, and then we will pick an unassigned red square. Next, we can pick a numbered square adjacent to it. We can try assigning mines in all possible locations around that number square. This will guarantee that that square will have its conditions satisfied, preventing the inefficiencies of the naive \(2^n\) possibilities approach.
Below is a visualisation of all mine possibilities around a central 2.
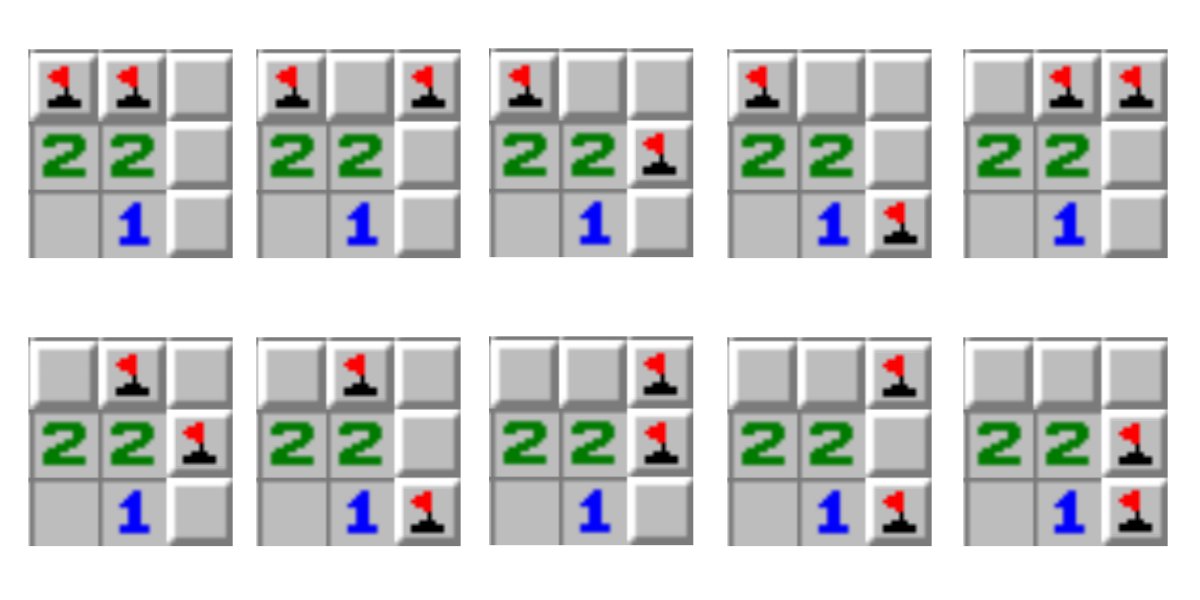
To further optimise this, we can also check the current assignment of mines every single time we do this. This will make sure that everything is satisfied at each stage of the recursion, stopping the algorithm from continuing down fruitless recursions, further optimising the algorithm.
When this recursion finds a valid possibility, it will represent a positioning of mines in uncovered squares that we have information on. As we go through and find more and more possibilities, we keep a count of how many possibilities have a mine in each cell.
If a cell has a mine in every single possibility we enumerate, it must contain a mine, and if it contains a mine in no possibilities, it must be mine-free.
The final optimization I have made is splitting the board into independent segments.

The segments are disconnected, and thus the choices in them aren’t relevant to each other. Considering them separately in my algorithm will create a huge exponential speedup. Previously, for each possible assignment of mines to, for example, the blue area, the algorithm would walk through all possible assignments of mines to the green area, even through they are unrelated. This optimisation is very effective as instead of considering the product of the number of possibilities in the blue, red, green and yellow and areas, I will only have to consider the sum of the number of possibilities.
The implementation
First, I will begin by declaring some classes.
The first is a coord class. This can store an x and y coordinate, but also has a unique string representation that will be useful later when it is used in maps. It also has a neighbourhood function that will return coordinates of all adjacent cells.
class coord {
constructor(x, y) {
if (typeof (x) === 'string') {
let xcp = x; // xcp secret laboratory
x = parseInt(xcp.split("-")[0]);
y = parseInt(xcp.split("-")[1]);
}
this.x = x;
this.y = y;
}
str() {
return "" + this.x + "-" + this.y;
}
neighbourhood(width, height) {
let neighbours = [];
for (let i = -1; i <= 1; i++) {
for (let j = -1; j <= 1; j++) {
let newx = this.x + i;
let newy = this.y + j;
if (newx >= 0 && newx < width &&
newy >= 0 && newy < height &&
!(i == 0 && j == 0)) {
neighbours.push(new coord(newx, newy));
}
}
}
return neighbours;
}
}I also create a Board class that will store the data of a minesweeper board.
class Board {
constructor(width, height, bombs) {
this.grid = []; // 1 = bomb, 0 = empty
this.width = width;
this.height = height;
this.bombs = bombs;
this.scannedGrid = [];
for (let i = 0; i < height; i++) {
this.scannedGrid.push([]);
this.grid.push([]);
for (let j = 0; j < width; j++) {
this.grid[this.grid.length - 1].push(0);
this.scannedGrid[this.scannedGrid.length - 1].push(0);
}
}
// randomly place bombs
let randoms = n_randoms(bombs, 0, width * height);
for (let i = 0; i < bombs; i++) {
let index = randoms[i];
this.grid[(index - (index % width)) / height][index % width] = 1;
}
for (let i = 0; i < height; i++) {
for (let j = 0; j < width; j++) {
this.scannedGrid[i][j] = this.probe(i, j);
}
}
}
getScan(loc) {
return this.scannedGrid[loc.y][loc.x];
}
getGrid(loc) {
return this.grid[loc.y][loc.x];
}
print() {
console.log(this.grid.map((val) => val.join("")).join("\n"));
}
printScanned() {
console.log(this.scannedGrid.map((val) => val.map((val) => (val == -1 ? "#" : val)).join("")).join("\n"));
}
probe(x, y) {
// return -1 for bomb, 0-8 otherwise
if (this.grid[y][x] == 1) {
return -1;
}
else {
let count = 0;
for (let i = -1; i <= 1; i++) {
for (let j = -1; j <= 1; j++) {
let newx = x + i;
let newy = y + j;
if (newx >= 0 && newx < this.width &&
newy >= 0 && newy < this.height) {
count += this.grid[newy][newx];
}
}
}
return count;
}
}
}I wrote this algorithm from the point of view of checking if a board has a deterministic solution. I've done this by adding a checkSolveable method to the Board class.
First, I initialise an unfilled copy of the board that the algorithm will use to store its current progress, and I find a 0 to initially select.
checkSolveable() {
let solverGrid = [];
for (let i = 0; i < this.height; i++) {
solverGrid.push([]);
for (let j = 0; j < this.width; j++) {
solverGrid[solverGrid.length - 1].push(-2);
}
}
let floodSolve = (point) => {
let seenPoints = new Map();
let floodSolveRec = (point) => {
solverGrid[point.y][point.x] = this.getScan(point);
seenPoints[point.str()] = true;
if (this.getScan(point) == 0) {
// scan around
for (let neighbour of point.neighbourhood(this.width, this.height)) {
if (seenPoints[neighbour.str()] == undefined) {
floodSolveRec(neighbour);
}
}
}
}
floodSolveRec(point);
}
function printSolverGrid() {
console.log(solverGrid.map((val) => val.map((val) => (val == -2 ? " " : (val == -1 ? "#" : val))).join("")).join("\n"));
}
// find a 0 to flood from
let zero;
let zeroes = [];
for (let i = 0; i < this.width; i++) {
for (let j = 0; j < this.height; j++) {
let c = new coord(i, j);
if (this.getScan(c) == 0) {
zeroes.push(c);
}
}
}
if (zeroes.length == 0) {
return {
solveable: false,
startcoord: null
};
}
else {
zero = zeroes[randomInteger(0, zeroes.length - 1)];
floodSolve(zero);
}Next, I begin writing a tear function that essentially makes deductions. The tear function is repeatedly called to go through the board and make deductions.
First, I will try to make simple deductions.
let tear = () => {
let bombsfoundcp = bombsfound;
let squarecleared = false;
let overallminplaced = 0;
for (let i = 0; i < this.height; i++) {
for (let j = 0; j < this.width; j++) {
if (solverGrid[i][j] != -2 && solverGrid[i][j] != -1) {
// check if you can be directly solved
let currcoord = new coord(j, i);
let currvalid = false;
let solverneighbours = currcoord.neighbourhood(this.width, this.height);
let total = solverGrid[i][j];
let coveredsurrounding = [];
let flaggedsurrounding = [];
let uncoveredsurrounding = [];
for (let solverneighbour of solverneighbours) {
if (solverGrid[solverneighbour.y][solverneighbour.x] == -2) {
coveredsurrounding.push(solverneighbour);
}
else if (solverGrid[solverneighbour.y][solverneighbour.x] == -1) {
flaggedsurrounding.push(solverneighbour);
}
else {
uncoveredsurrounding.push(solverneighbour);
}
}
if (total - flaggedsurrounding == 0) {
// go and uncover all empties
for (let neighbour of coveredsurrounding) {
squarecleared = true;
solverGrid[neighbour.y][neighbour.x] = this.getScan(neighbour);
if (solverGrid[neighbour.y][neighbour.x] < 0) {
console.log("MISTAKE " + neighbour.str());
}
}
}
if (total - flaggedsurrounding == coveredsurrounding.length) {
// go and flag all of those
for (let neighbour of coveredsurrounding) {
bombsfoundcp += 1;
solverGrid[neighbour.y][neighbour.x] = -1;
if (this.getScan(neighbour) != -1) {
console.log("MISTAKE " + neighbour.str());
}
}
}
}
}
}
if (squarecleared) {
bombsfound = bombsfoundcp;
return squarecleared;
}If this cannot make any progress, I begin by splitting the board into separate sections using a flood fill algorithm. I use Javascript Map() s to speed up some lookups. Javascript’s map is essentially a hash table, allowing for \(\mathcal{O}(\log{}n)\) insertions and lookups. This is useful, for example, in the flood fill, to prevent the recursion from revisiting cells that have already been visited.
let eqContributors = []; // array of coords
let eqContributorsMap = new Map();
let globalsolveMap = new Map();
for (let i = 0; i < this.height; i++) {
for (let j = 0; j < this.width; j++) {
if (solverGrid[i][j] != -2 && solverGrid[i][j] != -1) {
// check if you have a non-solved neighbourhood
let currcoord = new coord(j, i);
let currvalid = false;
let solverneighbours = currcoord.neighbourhood(this.width, this.height);
for (let solverneighbour of solverneighbours) {
if (solverGrid[solverneighbour.y][solverneighbour.x] == -2) {
// this is valid
if (!currvalid) {
currvalid = true;
eqContributors.push(currcoord);
eqContributorsMap[currcoord.str()] = true;
}
if (globalsolveMap[solverneighbour.str()] == undefined) {
globalsolveMap[solverneighbour.str()] = true;
}
}
}
}
}
}
// flood fill
let floodedMap = new Map();
let floodsCount = 0;
for (let contrib of eqContributors) {
if (floodedMap[contrib.str()] == undefined) {
floodsCount += 1;
// begin the flood. we'll use a queue
floodedMap[contrib.str()] = true;
let floodQueue = [contrib];
let contribFlood = [contrib];
while (floodQueue.length != 0) {
let newFloodQueue = [];
for (let c of floodQueue) {
let surroundings = c.neighbourhood(this.width, this.height);
for (let neighbour of surroundings) {
// we need to check if 1. we can go to this cell and 2. have we been to it before
// prohibit a jump from a solveMap to solveMap
if ((floodedMap[neighbour.str()] == undefined) && ((eqContributorsMap[neighbour.str()] != undefined) || (globalsolveMap[neighbour.str()] != undefined)) && !((globalsolveMap[neighbour.str()] != undefined) && (globalsolveMap[c.str()] != undefined))) {
newFloodQueue.push(neighbour);
floodedMap[neighbour.str()] = true;
if (eqContributorsMap[neighbour.str()] != undefined) {
contribFlood.push(neighbour);
}
}
}
}
floodQueue = newFloodQueue;
}
// contrib flood now has a list of contribs
// the flooding is working, yaya :)
// lets begin by creating new mapsI then try to perform the recursion algorithm on each group. The recursion is in a function called solveRec, and it takes a partial set of assignments of mines to covered cells, and tries to add new mines to these assignments. When it hits a valid assignment, it records it.
let minplaced = 9999999;
let validcount = 0;
let counts = [];
let solveRec = (assignments) => {
// here, the assignment needs to be pruned by checking it against equations that operate over the coords
// we add an n^2 factor for exponential speedup, so should be fine?
for (let j = 0; j < equations.length; j++) {
let eq = equations[j];
// go through the equation
let currsum = 0;
let completed = true;
for (let i = 0; i < eq.length; i++) {
if (eq[i] == 1) {
if (assignments[i] == -1) {
completed = false;
break;
}
else {
currsum += assignments[i];
}
}
}
if (completed) {
if (currsum !== slns[j]) {
// it's bad
return false;
}
}
}
// in assignments, -1 is unassigned, 0 assigned empty and 1 assigned bomb.
// find the index of an unassigned
let startidx = assignments.indexOf(-1);
if (startidx == -1) {
// the assignment is complete: now, it needs to be checked and return a true or false
validcount += 1;
let currsum = 0;
for (let i = 0; i < assignments.length; i++) {
counts[i] += assignments[i];
currsum += assignments[i];
}
if (currsum < minplaced) {
minplaced = currsum;
}
return true;
}
let currAssignment = contribFlood[solvToContri[revsolveMap[startidx]]];
let currNeigbours = currAssignment.neighbourhood(this.width, this.height);
let neighbourstoplace = []; // the indices in assignments that will get placed in
let numbertoplace = this.getScan(currAssignment);
// go through its neighbours
for (let neighbour of currNeigbours) {
// step 1: is this guy gonna be in assignments?
if (solveMap[neighbour.str()] != undefined) {
// well what is your assignment then
let assignidx = solveMap[neighbour.str()];
if (assignments[assignidx] == -1) {
neighbourstoplace.push(assignidx);
}
else if (assignments[assignidx] == 1) {
numbertoplace -= 1;
}
}
else {
// we should know about you
if (solverGrid[neighbour.y][neighbour.x] == -1) {
numbertoplace -= 1;
}
}
}
if (numbertoplace < 0 || numbertoplace > neighbourstoplace.length) {
return false;
}
// otherwise, lets go through new assignments
let combsRec = (soFar, soFarSum, n, k, cb) => {
if (soFar.length == n) {
cb(soFar);
}
else {
let cp1 = [...soFar];
let cp2 = [...soFar];
cp1.push(0);
cp2.push(1);
// can we add a 0? we can add a 0 if we have more space (n - sofar.length) than stuff that needs to be placed
let cannadd0 = ((n - soFar.length) > (k - soFarSum));
// we can add a 1 if we haven't placed k already
let cannadd1 = (soFarSum < k);
//console.log(JSON.stringify(soFar) + " " + soFarSum + " " + n + " " + k + " " + cannadd0 + " " + cannadd1)
if (cannadd0) {
combsRec(cp1, soFarSum, n, k, cb);
}
if (cannadd1) {
combsRec(cp2, soFarSum + 1, n, k, cb);
}
}
}
// combsRec([], 0, neighbourstoplace.length, numbertoplace, (placing) => {
// console.log("placing:")
// console.log(placing);
// });
combsRec([], 0, neighbourstoplace.length, numbertoplace, (placing) => {
// create a new assignment and recurse
let assignmentsCp = [...assignments];
for (let k = 0; k < placing.length; k++) {
assignmentsCp[neighbourstoplace[k]] = placing[k];
}
solveRec(assignmentsCp);
})
}Finally, a method to make deductions is if we know that covered squares will be empty through some mine count logic. If we know that the mines that would be in the squares that we are trying to work out will have enough bombs (minplaced) to guarantee that all remaining cells are empty, we can clear all of them.
let bombsleft = this.bombs - bombsfound;
if (overallminplaced == bombsleft) {
// every single other square can be uncovered
for (let i = 0; i < this.height; i++) {
for (let j = 0; j < this.width; j++) {
let coordtoclear = new coord(j, i);
if (solverGrid[i][j] == -2 && globalsolveMap[coordtoclear.str()] == undefined) {
squarecleared = true;
solverGrid[i][j] = this.getScan(coordtoclear);
}
}
}
}
bombsfound = bombsfoundcp;This works out to this final complete program.
// by Ojas Gulati
function randomInteger(min, max) {
return Math.floor(Math.random() * (max - min + 1)) + min;
}
function n_randoms(n, rangemin, rangemax) { // rangemax excluded
function shuffle(array) {
var currentIndex = array.length, temporaryValue, randomIndex;
// While there remain elements to shuffle...
while (0 !== currentIndex) {
// Pick a remaining element...
randomIndex = Math.floor(Math.random() * currentIndex);
currentIndex -= 1;
// And swap it with the current element.
temporaryValue = array[currentIndex];
array[currentIndex] = array[randomIndex];
array[randomIndex] = temporaryValue;
}
return array;
}
let shuff = [];
for (let i = rangemin; i < rangemax; i++) {
shuff.push(i);
}
shuff = shuffle(shuff);
let results = [];
for (let i = 0; i < n; i++) {
results.push(shuff[i]);
}
return results;
}
class coord {
constructor(x, y) {
if (typeof (x) === 'string') {
let xcp = x; // xcp secret laboratory
x = parseInt(xcp.split("-")[0]);
y = parseInt(xcp.split("-")[1]);
}
this.x = x;
this.y = y;
}
str() {
return "" + this.x + "-" + this.y;
}
neighbourhood(width, height) {
let neighbours = [];
for (let i = -1; i <= 1; i++) {
for (let j = -1; j <= 1; j++) {
let newx = this.x + i;
let newy = this.y + j;
if (newx >= 0 && newx < width &&
newy >= 0 && newy < height &&
!(i == 0 && j == 0)) {
neighbours.push(new coord(newx, newy));
}
}
}
return neighbours;
}
}
// create a board
class Board {
constructor(width, height, bombs) {
this.grid = []; // 1 = bomb, 0 = empty
this.width = width;
this.height = height;
this.bombs = bombs;
this.scannedGrid = [];
for (let i = 0; i < height; i++) {
this.scannedGrid.push([]);
this.grid.push([]);
for (let j = 0; j < width; j++) {
this.grid[this.grid.length - 1].push(0);
this.scannedGrid[this.scannedGrid.length - 1].push(0);
}
}
// randomly place bombs
let randoms = n_randoms(bombs, 0, width * height);
for (let i = 0; i < bombs; i++) {
let index = randoms[i];
this.grid[(index - (index % width)) / height][index % width] = 1;
}
for (let i = 0; i < height; i++) {
for (let j = 0; j < width; j++) {
this.scannedGrid[i][j] = this.probe(i, j);
}
}
}
getScan(loc) {
return this.scannedGrid[loc.y][loc.x];
}
getGrid(loc) {
return this.grid[loc.y][loc.x];
}
print() {
console.log(this.grid.map((val) => val.join("")).join("\n"));
}
printScanned() {
console.log(this.scannedGrid.map((val) => val.map((val) => (val == -1 ? "#" : val)).join("")).join("\n"));
}
probe(x, y) {
// return -1 for bomb, 0-8 otherwise
if (this.grid[y][x] == 1) {
return -1;
}
else {
let count = 0;
for (let i = -1; i <= 1; i++) {
for (let j = -1; j <= 1; j++) {
let newx = x + i;
let newy = y + j;
if (newx >= 0 && newx < this.width &&
newy >= 0 && newy < this.height) {
count += this.grid[newy][newx];
}
}
}
return count;
}
}
// by Ojas Gulati
checkSolveable() {
let solverGrid = [];
for (let i = 0; i < this.height; i++) {
solverGrid.push([]);
for (let j = 0; j < this.width; j++) {
solverGrid[solverGrid.length - 1].push(-2);
}
}
let floodSolve = (point) => {
let seenPoints = new Map();
let floodSolveRec = (point) => {
solverGrid[point.y][point.x] = this.getScan(point);
seenPoints[point.str()] = true;
if (this.getScan(point) == 0) {
// scan around
for (let neighbour of point.neighbourhood(this.width, this.height)) {
if (seenPoints[neighbour.str()] == undefined) {
floodSolveRec(neighbour);
}
}
}
}
floodSolveRec(point);
}
function printSolverGrid() {
console.log(solverGrid.map((val) => val.map((val) => (val == -2 ? " " : (val == -1 ? "#" : val))).join("")).join("\n"));
}
// find a 0 to flood from
let zero;
let zeroes = [];
for (let i = 0; i < this.width; i++) {
for (let j = 0; j < this.height; j++) {
let c = new coord(i, j);
if (this.getScan(c) == 0) {
zeroes.push(c);
}
}
}
if (zeroes.length == 0) {
return {
solveable: false,
startcoord: null
};
}
else {
zero = zeroes[randomInteger(0, zeroes.length - 1)];
floodSolve(zero);
}
let bombsfound = 0;
// now, find our bleeding edge and begin to tear it open
let tear = () => {
// by Ojas Gulati
let bombsfoundcp = bombsfound;
let squarecleared = false;
let overallminplaced = 0;
for (let i = 0; i < this.height; i++) {
for (let j = 0; j < this.width; j++) {
if (solverGrid[i][j] != -2 && solverGrid[i][j] != -1) {
// check if you can be directly solved
let currcoord = new coord(j, i);
let currvalid = false;
let solverneighbours = currcoord.neighbourhood(this.width, this.height);
let total = solverGrid[i][j];
let coveredsurrounding = [];
let flaggedsurrounding = [];
let uncoveredsurrounding = [];
for (let solverneighbour of solverneighbours) {
if (solverGrid[solverneighbour.y][solverneighbour.x] == -2) {
coveredsurrounding.push(solverneighbour);
}
else if (solverGrid[solverneighbour.y][solverneighbour.x] == -1) {
flaggedsurrounding.push(solverneighbour);
}
else {
uncoveredsurrounding.push(solverneighbour);
}
}
if (total - flaggedsurrounding == 0) {
// go and uncover all empties
for (let neighbour of coveredsurrounding) {
squarecleared = true;
solverGrid[neighbour.y][neighbour.x] = this.getScan(neighbour);
}
}
if (total - flaggedsurrounding == coveredsurrounding.length) {
// go and flag all of those
for (let neighbour of coveredsurrounding) {
bombsfoundcp += 1;
solverGrid[neighbour.y][neighbour.x] = -1;
}
}
}
}
}
if (squarecleared) {
bombsfound = bombsfoundcp;
return squarecleared;
}
let eqContributors = []; // array of coords
let eqContributorsMap = new Map();
let globalsolveMap = new Map();
for (let i = 0; i < this.height; i++) {
for (let j = 0; j < this.width; j++) {
if (solverGrid[i][j] != -2 && solverGrid[i][j] != -1) {
// check if you have a non-solved neighbourhood
let currcoord = new coord(j, i);
let currvalid = false;
let solverneighbours = currcoord.neighbourhood(this.width, this.height);
for (let solverneighbour of solverneighbours) {
if (solverGrid[solverneighbour.y][solverneighbour.x] == -2) {
// this is valid
if (!currvalid) {
currvalid = true;
eqContributors.push(currcoord);
eqContributorsMap[currcoord.str()] = true;
}
if (globalsolveMap[solverneighbour.str()] == undefined) {
globalsolveMap[solverneighbour.str()] = true;
}
}
}
}
}
}
// flood fill
let floodedMap = new Map();
let floodsCount = 0;
for (let contrib of eqContributors) {
if (floodedMap[contrib.str()] == undefined) {
floodsCount += 1;
// begin the flood. we'll use a queue
floodedMap[contrib.str()] = true;
let floodQueue = [contrib];
let contribFlood = [contrib];
while (floodQueue.length != 0) {
let newFloodQueue = [];
for (let c of floodQueue) {
let surroundings = c.neighbourhood(this.width, this.height);
for (let neighbour of surroundings) {
// we need to check if 1. we can go to this cell and 2. have we been to it before
// prohibit a jump from a solveMap to solveMap
if ((floodedMap[neighbour.str()] == undefined) && ((eqContributorsMap[neighbour.str()] != undefined) || (globalsolveMap[neighbour.str()] != undefined)) && !((globalsolveMap[neighbour.str()] != undefined) && (globalsolveMap[c.str()] != undefined))) {
newFloodQueue.push(neighbour);
floodedMap[neighbour.str()] = true;
if (eqContributorsMap[neighbour.str()] != undefined) {
contribFlood.push(neighbour);
}
}
}
}
floodQueue = newFloodQueue;
}
// contrib flood now has a list of contribs
// the flooding is working, yaya :)
// lets begin by creating new maps
let solveMap = new Map();
let revsolveMap = new Map();
let solvToContri = new Map();
let equations = [];
let slns = [];
let currSolve = 0;
for (let i = 0; i < contribFlood.length; i++) {
let c = contribFlood[i];
let neighbourhood = c.neighbourhood(this.width, this.height);
for (let neighbour of neighbourhood) {
if (solverGrid[neighbour.y][neighbour.x] == -2) {
if (solveMap[neighbour.str()] == undefined) {
solveMap[neighbour.str()] = currSolve;
solvToContri[neighbour.str()] = i;
revsolveMap[currSolve] = neighbour.str();
currSolve += 1;
}
}
}
}
// now build the equations
for (let i = 0; i < contribFlood.length; i++) {
let solverneighbours = contribFlood[i].neighbourhood(this.width, this.height);
let sumTarget = this.getScan(contribFlood[i]);
let idxmap = new Map();
let neighboursused = [];
for (let neighbour of solverneighbours) {
if (solverGrid[neighbour.y][neighbour.x] == -1) {
sumTarget -= 1;
}
else if (solverGrid[neighbour.y][neighbour.x] == -2) {
idxmap[solveMap[neighbour.str()]] = true;
neighboursused.push(neighbour);
}
}
let eq = [];
for (let j = 0; j < currSolve; j++) {
if (idxmap[j] == undefined) {
eq.push(0);
}
else {
eq.push(1);
}
}
equations.push(eq);
//console.log(JSON.stringify(eq) + " " + sumTarget);
slns.push(sumTarget)
}
// now each bleeding edge equare has a number from [0, currSolve)
// here, go through the bleeding edges and assign them numbers
let minplaced = 9999999;
let validcount = 0;
let counts = [];
let solveRec = (assignments) => {
// here, the assignment needs to be pruned by checking it against equations that operate over the coords
// we add an n^2 factor for exponential speedup, so should be fine?
for (let j = 0; j < equations.length; j++) {
let eq = equations[j];
// go through the equation
let currsum = 0;
let completed = true;
for (let i = 0; i < eq.length; i++) {
if (eq[i] == 1) {
if (assignments[i] == -1) {
completed = false;
break;
}
else {
currsum += assignments[i];
}
}
}
if (completed) {
if (currsum !== slns[j]) {
// it's bad
return false;
}
}
}
// in assignments, -1 is unassigned, 0 assigned empty and 1 assigned bomb.
// find the index of an unassigned
let startidx = assignments.indexOf(-1);
if (startidx == -1) {
// the assignment is complete: now, it needs to be checked and return a true or false
validcount += 1;
let currsum = 0;
for (let i = 0; i < assignments.length; i++) {
counts[i] += assignments[i];
currsum += assignments[i];
}
if (currsum < minplaced) {
minplaced = currsum;
}
return true;
}
let currAssignment = contribFlood[solvToContri[revsolveMap[startidx]]];
let currNeigbours = currAssignment.neighbourhood(this.width, this.height);
let neighbourstoplace = []; // the indices in assignments that will get placed in
let numbertoplace = this.getScan(currAssignment);
// go through its neighbours
for (let neighbour of currNeigbours) {
// step 1: is this guy gonna be in assignments?
if (solveMap[neighbour.str()] != undefined) {
// well what is your assignment then
let assignidx = solveMap[neighbour.str()];
if (assignments[assignidx] == -1) {
neighbourstoplace.push(assignidx);
}
else if (assignments[assignidx] == 1) {
numbertoplace -= 1;
}
}
else {
// we should know about you
if (solverGrid[neighbour.y][neighbour.x] == -1) {
numbertoplace -= 1;
}
}
}
if (numbertoplace < 0 || numbertoplace > neighbourstoplace.length) {
return false;
}
// otherwise, lets go through new assignments
let combsRec = (soFar, soFarSum, n, k, cb) => {
if (soFar.length == n) {
cb(soFar);
}
else {
let cp1 = [...soFar];
let cp2 = [...soFar];
cp1.push(0);
cp2.push(1);
// can we add a 0? we can add a 0 if we have more space (n - sofar.length) than stuff that needs to be placed
let cannadd0 = ((n - soFar.length) > (k - soFarSum));
// we can add a 1 if we haven't placed k already
let cannadd1 = (soFarSum < k);
//console.log(JSON.stringify(soFar) + " " + soFarSum + " " + n + " " + k + " " + cannadd0 + " " + cannadd1)
if (cannadd0) {
combsRec(cp1, soFarSum, n, k, cb);
}
if (cannadd1) {
combsRec(cp2, soFarSum + 1, n, k, cb);
}
}
}
// combsRec([], 0, neighbourstoplace.length, numbertoplace, (placing) => {
// console.log("placing:")
// console.log(placing);
// });
combsRec([], 0, neighbourstoplace.length, numbertoplace, (placing) => {
// create a new assignment and recurse
let assignmentsCp = [...assignments];
for (let k = 0; k < placing.length; k++) {
assignmentsCp[neighbourstoplace[k]] = placing[k];
}
solveRec(assignmentsCp);
})
}
let initAssign = [];
for (let j = 0; j < currSolve; j++) {
initAssign.push(-1);
counts.push(0);
}
solveRec(initAssign);
//console.log(validcount);
//console.log(minplaced);
//console.log(counts);
for (let i = 0; i < counts.length; i++) {
if (counts[i] == validcount) {
// this square can be flagged
let c = new coord(revsolveMap[i]);
solverGrid[c.y][c.x] = -1;
bombsfoundcp += 1;
}
else if (counts[i] == 0) {
let c = new coord(revsolveMap[i]);
squarecleared = true;
solverGrid[c.y][c.x] = this.getScan(c); // we can uncover this square
}
}
overallminplaced += minplaced;
}
}
let bombsleft = this.bombs - bombsfound;
if (overallminplaced == bombsleft) {
// every single other square can be uncovered
for (let i = 0; i < this.height; i++) {
for (let j = 0; j < this.width; j++) {
let coordtoclear = new coord(j, i);
if (solverGrid[i][j] == -2 && globalsolveMap[coordtoclear.str()] == undefined) {
squarecleared = true;
solverGrid[i][j] = this.getScan(coordtoclear);
}
}
}
}
bombsfound = bombsfoundcp;
// if (validcount > 200) {
// console.log(validcount);
// printSolverGrid();
// }
//printSolverGrid();
return squarecleared;
}
let res = true;
while (res && bombsfound != this.bombs) {
res = tear();
// printSolverGrid();
//console.log(res);
}
return {
solveable: bombsfound == this.bombs,
startcoord: zero
}
}
}Some benchmarking
This algorithm can check through 100,000 8x8 boards with 13 mines in 101 seconds.
Out of these randomly generated boards, 33.8% are solvable deterministically.
This algorithm can also check through 1,000 20x20 boards with 80 mines in 17.8 seconds.
Out of these randomly generated boards, 23.6% are solvable deterministically.
Further improvements
Obviously, I could try some form of linear algebra to speed up solves, but this may lose the probability analysis potential.
Currently, I scan the board every iteration to find the cells on the edge, but I can deduce this from what cells are uncovered at each iteration.
I could try using the number of combinations (the counts array) to calculate probabilities of cells having a mine by looking at # possibilities where a cell has a mine / # where it doesn’t. I could also implement logic to assign a probability that a cell that we have no information on has a mine in it.
Finally, my checking of if a solution is valid is still loosely based on a linear algebra implementation, and so it checks way more squares than it actually needs to.
Help me with a future article
You will have to draw pictures in the square box from the prompts given in a limited amount of time and ink. As time goes on, your level will increase and you will have less time to draw.
Please try to keep the drawings close enough to the actual prompt - skip if something is too hard to draw.
Press begin to start the game :)
If you choose to enter a name, it may be displayed with your drawings on the internet.
Ready to draw?
Drawings:
0