Simulating simple molecular structures with Three.js - part 1: basic repulsion

This article has definitely been in the works for the longest amount of time, and will be split into two parts. This article covers a simple simulation of repelling electron pairs around an atom, and the next article will extend this to simulate small molecules.

This project started with a desire to think about the VSEPR atomic structure model.

A brief introduction to the VSEPR model

In VSEPR, bonding in atoms is simulated by the repulsion by pairs of electrons. All electrons pair up in bonds and “repel” each other in order to maximise their distance from each other. If the distance between bonding atoms is maximised, the energy of the system will be minimized, as there will be the least repulsive force between electrons. Lone pairs have a slightly higher repulsion as they are “closer” to the nucleus.

This model is very good at explaining all kinds of complex structures, but at first, I just wanted to think about it in a single atom.

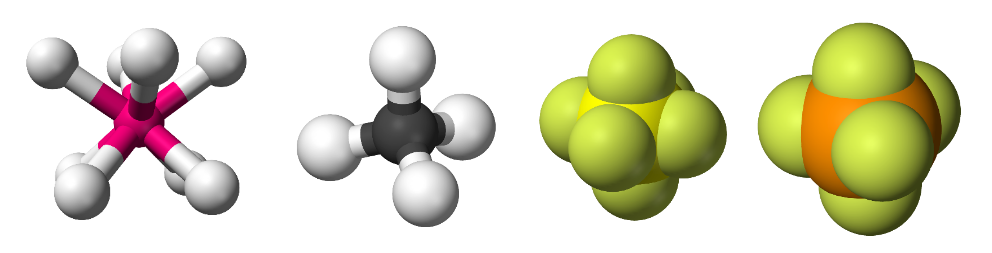
VSEPR in a single, simple molecule

At first, I was content with simulating this spreading in a single atom.
In principle, this is quite a simple task. Using Coulomb's law, I can give points around a sphere (representing electron pairs or ions) equal charges and simulate their repulsion.
As all points have the same charge, the charge term in Coulomb’s law disappears. I can then simply scale the force proportional to \(\frac{1}{distance^2}\).

Before we get ahead of ourselves, we should first think about how we would simulate forces.
This is a lot easier than it sounds. At each frame of the animation, I calculate the forces between every single pair of particles and sum these vectors to get a net force on each particle. Then, I can accelerate the particles by this force, storing their velocity along the way. Finally, I can increment the position of each particle by the velocity multiplied by how much time passes in a frame.

This requires me to declare two global constants:
forcemul - this is the proportionality constant in Coulomb's law. As we’re making our own universe, who says we can’t pick our own constants? ;)
frametime - this is how much time is considered to pass each frame, and thus by how much each particle’s position is incremented as a multiple of its velocity.

First, I begin by creating all the particles:

let pointslist = [];
const pointmaterial = new THREE.MeshPhysicalMaterial({
color: 0x0000ff,
roughness: 0.2
});

function placeOnSphere(vector, radius) {
return vector.normalize().multiplyScalar(radius);
}

let pointvecs = [];
let velocvecs = [];

let lines = [];
const linematerial = new THREE.LineBasicMaterial({
color: 0xffffff
});

for (let i = 0; i < pointscount; i++) {
const pointgeo = new THREE.SphereGeometry(0.1, 8, 8);
const point = new THREE.Mesh(pointgeo, pointmaterial);
pointslist.push(point);
scene.add(point);

// calculate the position
let posvec = []
for (let x = 0; x < 3; x++) {
    posvec.push((Math.random() * 2) - 1);
}
posvec = placeOnSphere(new THREE.Vector3(...posvec), sphereRadius);
pointvecs.push(posvec);
velocvecs.push((new THREE.Vector3(0, 0, 0))) // new declares are 0 vectors
console.log(velocvecs[i]);
point.position.copy(posvec);

lines.push([]);
}

for (let i = 0; i < pointscount; i++) {
    for (let j = 0; j < pointscount; j++) {
        if (i != j) {
            // make the line
    
            const points = [];
            points.push(pointvecs[i]);
            points.push(pointvecs[j]);
    
            const geometry = new THREE.BufferGeometry().setFromPoints(points);
    
            const line = new THREE.Line(geometry, linematerial);
            lines[i].push(line);
            scene.add(line);
        }
        else {
            lines[i].push(null);
        }
    }
}

 

Next, I apply forces and update velocities:

// step 1: figure out the forces on each point
let forcevecs = new Array(pointscount);
for (let i = 0; i < pointscount; i++) {
    forcevecs[i] = new THREE.Vector3(0, 0, 0);
}
for (let i = 0; i < pointscount; i++) {
    for (let j = 0; j < pointscount; j++) {
        if (i != j) {
            // we need a vector from the j point to the i point to get the direction of the force that j applies on i.
            let line = pointvecs[i].clone().sub(pointvecs[j]);
            let distance = line.length();
            let direction = line.normalize();
            let force = direction.multiplyScalar(forcemul / (distance * distance));
            forcevecs[i].add(force);
        }
    }

    // add a heat force
    forcevecs[i].add((new THREE.Vector3()).random().add(subtraction).multiplyScalar(options.heat));
}
// now that we know what acceleration each point feels, we need to update the speed of each point
for (let i = 0; i < pointscount; i++) {
    velocvecs[i].add(forcevecs[i].clone().multiplyScalar(frametime));
}

This runs in an animation loop that calls itself using the browser's requestAnimationFrame function.

Of course, that would result in particles flying off away from each other, so I instead keep the particles “clamped” onto a sphere. To do this, I simply position each particle to be on the point where the ray from the center to the particle intersects the sphere to be it on. I also project the velocity to be on a plane perpendicular to the ray from the particle to the center. I’ve illustrated this clamping below.

 

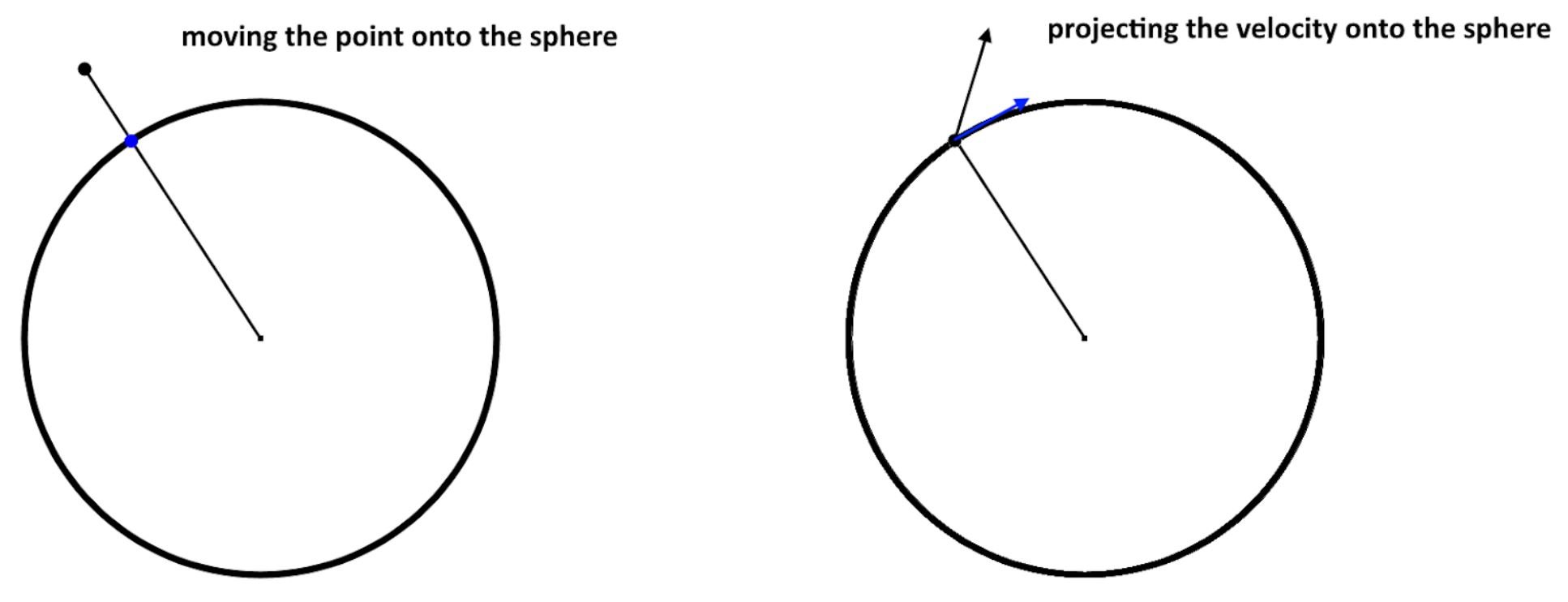
The point moving and position update is done here:

for (let i = 0; i < pointscount; i++) {
    pointvecs[i].add(velocvecs[i].clone().multiplyScalar(frametime)).normalize().multiplyScalar(sphereRadius);
}

And the velocity can easily be clamped using this function from the Three.js vector library:

for (let i = 0; i < pointscount; i++) {
    let planenormal = pointvecs[i].clone();
    velocvecs[i].projectOnPlane(planenormal);
}

Before I moved on, I wanted to show what 3D shape these points would make. This required something called a convex hull algorithm. This creates the smallest shape around a set of points that is convex. As my points are all on a sphere, all points are part of this shape.
Analysing these algorithms was a huge time sink in this project, as I attempted to implement a full quickhull algorithm. This article was about to be about a convex hull algorithm, until I realised how difficult implementing this was, and how it seemed like only 3 people in the whole world had ever implemented this and everyone else had just ported and optimised the same base code.

After spending a few days in this rabbit hole, I eventually moved to Three.js’s built-in convex hull algorithm. However, to do this, I would also need to continually run the convex hull algorithm and update a BufferGeometry that would display the hull.

This was accomplished with the following code:

function updateHullGeom(mesh, hull) {
    let geom = mesh.geometry;
    var vertices = [];
    var normals = [];
    var faces = hull.faces;
    for (var i = 0; i < faces.length; i++) {
        var face = faces[i];
        var edge = face.edge;
        do {
            var point = edge.head().point;
            vertices.push(point.x, point.y, point.z);
            normals.push(face.normal.x, face.normal.y, face.normal.z);
            edge = edge.next;
        } while (edge !== face.edge);
    }
    // build geometry
    geom.setAttribute('position', new THREE.Float32BufferAttribute(vertices, 3));
    geom.setAttribute('normal', new THREE.Float32BufferAttribute(normals, 3));
    geom.attributes.position.needsUpdate = true;
}
 
let hullgeometry = new THREE.BufferGeometry();
let convexHull = new THREE.ConvexHull().setFromPoints(pointvecs);
const hullmaterial = new THREE.MeshPhysicalMaterial( {
    color: 0xffffff
});
const hullmesh = new THREE.Mesh(hullgeometry, hullmaterial);
updateHullGeom(hullmesh, convexHull);
scene.add(hullmesh);

This code creates a geometry for the hull and a mesh. The updateHullGeom method copies the geometry created from the Three.js convex hull algorithm and copies it into a single object. This saves the overhead of continually redeclaring Three geometries.

Fixing some issues with the system

This simulation did have a few pressing issues though.
One problem was that particles could accumulate really high velocities and not slow down.

To deal with this problem, I would have to introduce frictions.
For friction, I just used some simple yet effective mechanics principles.
First of all, I apply a sort of static friction. Every time step, I subtract a certain amount from the velocity. This wasn’t very effective, but remains implemented in the option staticfrictioncoeff.

What was instead much more effective was a dynamic friction.
The dynamic friction sets the velocity of each particle as a multiple of the current velocity each timestep. This causes velocities to exponentially decay, and can be adjusted to easily drop the velocity of all particles to 0 easily, while keeping the animation seeming smooth.
This is implemented in the option dynamicfrictioncoeff.

The final issue was one that I never actually implemented into the system, but more an insurance for the future. This is a heat option. In the real world, heat is “microscopic kinetic energy”. Particles oscillate randomly on their positions due to heat. This can easily be implemented by adding a small random force to each particle each time step. The heat parameter is useful for many reasons. For example, if all particles are in a plane, all force vectors will be in that plane, and they will arrange themselves into a metastable configuration (a ring). The heat forces nudge the particles out of the metastable configuration of the ring and into more stable configurations.

One interesting activity is using the heat empirically, to see how much heat it takes to destabilize a structure, as I will show later.

Adding UI

The dat.GUI module provided by Google gives a way to easily create GUIs to adjust the parameters in this system. In this application, there is a UI option for each of the previously mentioned parameters: forcemul, staticfrictioncoeff, dynamicfrictioncoeff, frametime and heat.

The final tool

Use your mouse to rotate around the simulation.

Points: Simulate

 

Experiments on stability

As previously mentioned, heat is a good way to measure the stability of these configurations. This allows me to use this tool to effectively perform “experiments” on this structure.

I explore this a little bit in the following YouTube video:

This repulsion system also sets the foundations for my molecule simulation system, coming in the next article.